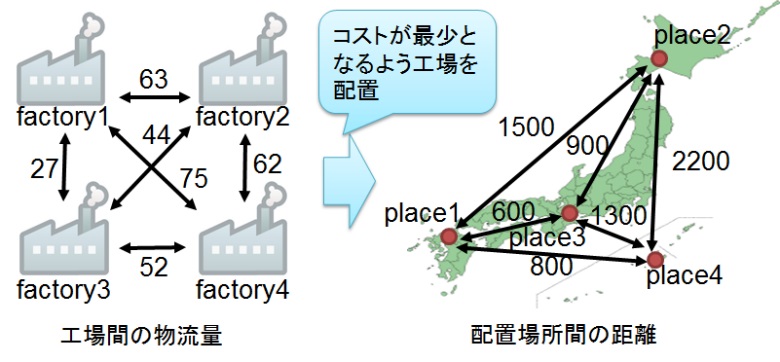
組合せ最適化問題には、ネットワーク設計問題、配送計画問題、施設配置問題（図1）、スケジューリング問題などがあり、社会に現れる現実問題の多くが組合せ最適化問題として定式化できます。企業においても、製品開発やシステム開発で、組合せ最適化問題を解かなければならない事例が数多く存在します。これら組合せ最適化問題の多くは、問題の規模が大きい場合に厳密に最適解を求めることが極めて困難であるNP困難な問題として、計算の複雑さの理論により明らかにされてきました。NP困難な問題では、問題サイズが大きくなると組合せ数が爆発的に増加するため（図2）、すべての組合せを調べることは現実的ではありません。本研究室では、このようなNP困難な問題に対して、現実的な時間内にできるだけよい近似解を求めることを目的とした、進化計算などのメタ戦略を用いたアルゴリズムの開発を行っています。NP困難な問題の中でも、さらに難しい、大規模な組合せ最適化問題（約10³⁰⁰⁰⁰通りの組合せ）に関する研究を行っています。